If you have not done ‘Nzepple before, you can find out more
about it Here.
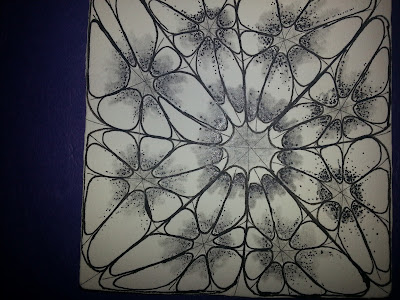
And here is My ‘Nzeppel Zentangle® Tile!
Some of the reasons I like the number nine… (Yoinked from
Wikipedia)
Nine is a composite number, its proper divisors being 1 and
3. It is 3 times 3 and hence the third square number. Nine is a Motzkin number.
It is the first composite lucky number, along with the first composite odd
number.
Nine is the highest single-digit number in the decimal
system. It is the second non-unitary square prime of the form (p2) and the
first that is odd. All subsequent squares of this form are odd. It has a unique
aliquot sum 4 which is itself a square prime. Nine is; and can be, the only
square prime with an aliquot sum of the same form. The aliquot sequence of nine
has 5 members (9,4,3,1,0) this number being the second composite member of the
3-aliquot tree. It is the aliquot sum of only one number the discrete semiprime
15.
There are nine Heegner numbers.
Since 9 = 321, 9 is an exponential factorial.
8 and 9 form a Ruth-Aaron pair under the second definition
that counts repeated prime factors as often as they occur.
In bases 12, 18 and 24, nine is a 1-automorphic number and
in base 6 a 2-automorphic number (displayed as '13').
A polygon with nine sides is called a nonagon or enneagon] A
group of nine of anything is called an ennead.
In base 10 a number is divisible by nine if and only if its
digital root is 9. That is, if you multiply nine by any natural number, and
repeatedly add the digits of the answer until it is just one digit, you will
end up with nine:
2 × 9 = 18 (1 + 8 = 9)
3 × 9 = 27 (2 + 7 = 9)
9 × 9 = 81 (8 + 1 = 9)
121 × 9 = 1089 (1 + 0 + 8 + 9 = 18; 1 + 8 = 9)
234 × 9 = 2106 (2 + 1 + 0 + 6 = 9)
578329 × 9 = 5204961 (5 + 2 + 0 + 4 + 9 + 6 + 1 = 27; 2 + 7
= 9)
482729235601 × 9 = 4344563120409 (4 + 3 + 4 + 4 + 5 + 6 + 3
+ 1 + 2 + 0 + 4 + 0 + 9 = 45; 4 + 5 = 9)
There are other interesting patterns involving multiples of
nine:
12345679 x 9 = 111111111
12345679 x 18 = 222222222
12345679 x 81 = 999999999
This works for all the multiples of 9. n = 3 is the only
other n > 1 such that a number is divisible by n if and only if its digital
root is n. In base N, the divisors of N − 1 have this property. Another
consequence of 9 being 10 − 1, is that it is also a Kaprekar number.
The difference between a base-10 positive integer and the
sum of its digits is a whole multiple of nine. Examples:
The sum of the digits of 41 is 5, and 41-5 = 36. The digital
root of 36 is 3+6 = 9, which, as explained above, demonstrates that it is
divisible by nine.
The sum of the digits of 35967930 is 3+5+9+6+7+9+3+0 = 42,
and 35967930-42 = 35967888. The digital root of 35967888 is 3+5+9+6+7+8+8+8 =
54, 5+4 = 9.
Subtracting two base-10 positive integers that are
transpositions of each other yields a number that is a whole multiple of nine.
Examples:
41 - 14 = 27 (2 + 7 = 9)
36957930 - 35967930 = 990000, a multiple of nine.
This works regardless of the number of digits that are
transposed. For example, the largest transposition of 35967930 is 99765330 (all
digits in descending order) and its smallest transposition is 03356799 (all
digits in ascending order); subtracting pairs of these numbers produces:
99765330 - 35967930 = 63797400; 6+3+7+9+7+4+0+0 = 36; 3+6 =
9.
99765330 - 03356799 = 96408531; 9+6+4+0+8+5+3+1 = 36; 3+6 =
9.
35967930 - 03356799 = 32611131; 3+2+6+1+1+1+3+1 = 18; 1+8 =
9.
Casting out nines is a quick way of testing the calculations
of sums, differences, products, and quotients of integers, known as long ago as
the 12th Century.
Every prime in a Cunningham chain of the first kind with a
length of 4 or greater is congruent to 9 mod 10 (the only exception being the
chain 2, 5, 11, 23, 47).
Six recurring nines appear in the decimal places 762 through
767 of pi. This is known as the Feynman point.
If an odd perfect number is of the form 36k + 9, it has at
least nine distinct prime factors.
If you divide a number by the amount of 9s corresponding to
its number of digits, the number is turned into a repeating decimal. (e.g.
274/999 = 0.274274274274...)
Nine is the binary complement of number six:
9 = 1001
6 = 0110
Like your shading and the stippling that you did. 'Nzeppel is one of my favorite tangles.
ReplyDeleteSorry about the double link. Hit the wrong key. The one for this challenge is #4
DeleteI love your 'Nzeppel Roy. I like the (vague) contrast.
ReplyDeleteAnd I owe you a BIG thank you for making me draw this difficult tangle.
I am glad that you kind of, nicely of course, force us into doing somethings that we don't particularly like. I think we don't like them because we can't do them. This challenge makes us pay attention, and then we find out we actually like the tangle. Thanks again also, Roy, for being so kind about my sensitive ears :)
ReplyDeleteI don't think this will ever be one of my favorite tangles, but I'm like Jean, I have to thank you Roy for making me think outside my comfort zone and learn something new to me. That's one reason I like to participate in challenges they keep me from falling into only what comfortable.
ReplyDeleteThanks again, Roy! I really enjoy your blog :)
ReplyDeleteAll done! This one was more challenging to get a unique take.
ReplyDeleteOne of my favourite tangles - thanks Roy, had fun with this one :)
ReplyDeleteThanks for introducing to me to this tangle! It has quickly become a new favorite of mine.
ReplyDeleteand I didn't mean to double link. I thought I mis-clicked the first time. If you're able to delete entries go ahead and delete my first one. It was the wrong link anyway. It jumps to my comment section instead of the top of my post.
ReplyDelete